“九章”问世：量子计算机究竟有多快（三）

量子计算究竟是如何工作的

　　这个问题涉及的是量子计算机的基本原理， 包括叠加态原理，量子纠缠， 量子态空间的高维性，以及量子干涉。

　　叠加态原理是说如果一个量子系统可以处在两个可区分状态中的一种，那么它也可以同时处在这两种状态上，即它可以处在叠加态上。如下图所示，其中 和 是复数， 并且它们模的平方和为1，这叫做波恩定则。如果你对这个系统进行测量，看它是处在量子态A还是量子态B，得到状态A的概率是|α|平方，得到状态B的概率是|β|平方。

　　下面讲一下数学中的叠加态原理，量子态可以用复向量空间中的单位向量来表示，当两个量子态可以用两个正交向量表示，它们就是可区分的。

　　量子比特就是一个有两个可区分状态的量子系统。

　　一个常见的例子就是极化光子， 它只有两个可区分的极化方向： 垂直极化和水平极化。一个极化光子，你只能看到垂直极化或水平极化，其他的所有状态都可由这两种状态产生。比如右对角极化是垂直极化加上水平极化，左对角极化是水平极化减去垂直极化，也有右旋圆极化，其中相位滞后90度。

　　这听起来比较奇怪， 但量子力学就是如此奇怪。如果你有两个量子比特，那么它们就可以处在4种状态的叠加，现在不用水平极化和垂直极化来代表两种可区分状态，而是用0态和1态来表示，比如这种两比特状态， |01>-|10>，其中每个量子比特都没有确定的状态。

　　当两个量子系统从整体上看处在确定的状态， 但分开看却处在不确定的状态时，它们是纠缠的。这就是令爱因斯坦不安的地方， 他把这个称为“鬼魅般的超距作用”。许多其他著名的科学家也对此感到困惑，纠缠为什么令人不安呢？如果你用概率论来解释，这就导致了所谓的局域实在论。你将不得不接受这样一个结论：在一个地方进行的测量， 会影响到另外一个地方的测量结果，尽管这两个地点间没有任何联系，你可以认为它们分开的足够远。

　　如何解决这个问题呢？一种办法就是去接受这种“鬼魅般的超距作用”，另一种方法是承认量子力学中的概率定律与经典情况不同。量子力学可以加速计算的第三个特性是量子系统的高维性，如果你有n个量子比特， 则它们的量子态由一个2的n次方维的向量描述。下面这些就是这个向量空间的基矢。

　　量子计算机的线路模型

　　这个空间的高维性也是量子计算拥有强大计算能力的原因之一。而量子计算机的线路模型是一个简化模型，就像图灵机的简化模型一样。不过一些量子计算机并不是严格的线路模型，它们会有些不同，不过这是一个很好的方式去理解量子计算机。

　　为了进行计算，我们需要给计算机输入， 需要改变计算机的状态，需要获取计算机的输出。那么如何做到这些呢？ 对于输入，我们可以在二进制输入对应的状态下启动计算机， 比如，100101101， 我们把第一个量子比特置为1态，把第二个量子比特置为0态，其它量子比特同理置为某个状态。我们也许需要额外的空间来运行算法，所以我们需要在初始化时添加额外的0，就像这些0一样需要更多的空间。

　　下面来看看如何输出。在计算结束时，量子计算机处在某种状态， 比如这种一般的量子态。但我们不能通过测量完全标定出量子态， 因为有海森堡不确定性原理。假设是在标准基下进行投影测量的，那么将会有||的概率得到结果i，比如你会有||的概率得到|0…001>，所以应该怎么做呢？

　　当观察量子计算机后却得到一个概率分布，且无法做得比这更好了，这是因为量子力学本质上是一种概率论。你肯定会问：那如何确定量子算法解决了问题呢？我们认为：当能够以很大概率得到正确结果时，该量子算法就解决了问题，这跟用经典概率算法解决问题一样。

　　现在我们需要引入量子力学的另外一个原理：线性原理，即孤立量子系统的演化是线性的。孤立量子系统中纯态的演化可以用作用在态空间上的密度矩阵来描述，干涉来源于量子态是用复数表示。

　　如果对0态施加一次H变换， 则各有50%几率得到0态或者1态，但是如果应用了两次变换，在这里就会有一个负号， 这就意味着|0>这一项抵消了。也就是说，施加两次变换后，|0>会变成|1>，|1>会变成-|0>，这就是量子计算运行的一个例子。

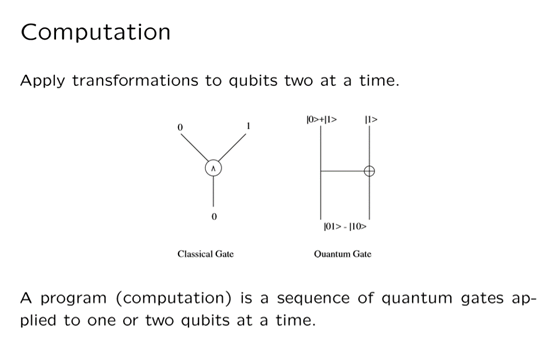
　　而说到计算，对单个或两个量子比特进行变换操作时， 相当于用2*2或4*4矩阵乘它们， 这跟经典计算机进行计算是类似的，即任何经典计算都由基本的与或非门组成。

　　

来源：新浪科技